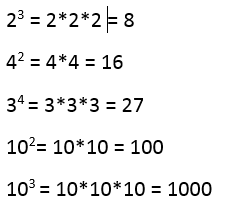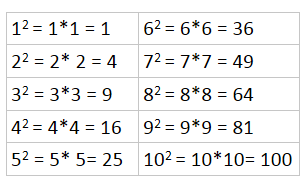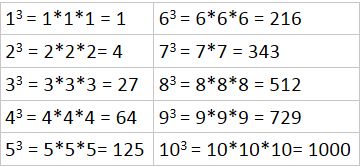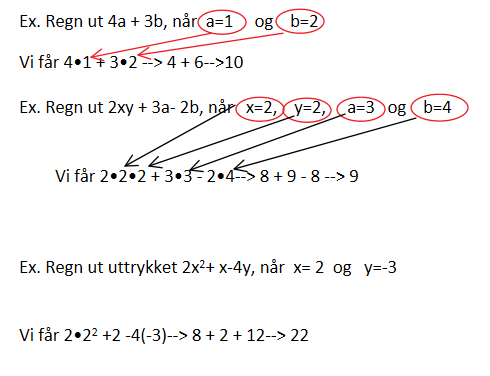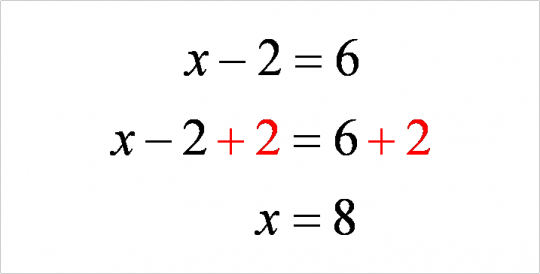Tall og algebra er et meget sentralt område i matematikken. Gode grunnleggende ferdigheter i disse emne er viktig for å kunne arbeide med - og forstå matematikk.
|
Tall |
|
Posisjonssystemet- Titallssystemet
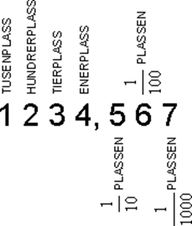
Tallsystemet vårt (titallsystemet) er et posisjonssystem der hvert siffer har en egen verdi. Vi kaller det enerplass, tierplass, hundredelsplass osv. Et siffer er ett tall. Tallet 365 har tre siffer. Vi har 5 enere, 6 tiere og 3 hundrere i dette tallet. Dette kan skrives på utvidet form; 3*100+ 6*10+ 5*1--> 365.
Tallsystemet vårt (titallsystemet) er et posisjonssystem der hvert siffer har en egen verdi. Vi kaller det enerplass, tierplass, hundredelsplass osv. Et siffer er ett tall. Tallet 365 har tre siffer. Vi har 5 enere, 6 tiere og 3 hundrere i dette tallet. Dette kan skrives på utvidet form; 3*100+ 6*10+ 5*1--> 365.
Tallinje
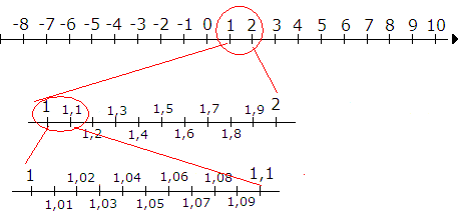
En tallinje gir et bilde av tallenes plassering i forhold til hverandre. I mange tilfeller er det lurt å tegne opp en tallinje for å kunne si noe om "avstanden" mellom ulike tall. Vi skiller mellom positive og negative tall.
En tallinje gir et bilde av tallenes plassering i forhold til hverandre. I mange tilfeller er det lurt å tegne opp en tallinje for å kunne si noe om "avstanden" mellom ulike tall. Vi skiller mellom positive og negative tall.
|
Som bildet til høyre viser finnes det uendelig mange tall mellom to valgte tall. Vi kan lage nye tall ved å legge til nye desimaler. |
|
De fire regnearter
Vi har fire regnearter som ligger til grunn i mange grener av matematikk.
Addisjon, subtraksjon, divisjon og multiplikasjon.
Vi har fire regnearter som ligger til grunn i mange grener av matematikk.
Addisjon, subtraksjon, divisjon og multiplikasjon.
|
Addisjon
ledd + ledd= sum 24 + 1,12 = 25,12 |
Subtraksjon
ledd - ledd = differanse 365 - 37 = 328 |
Multiplikasjon
faktor * faktor = produkt 9 * 8 = 72 |
Divisjon
dividend : divisor = kvotient 32 : 4 = 8 |
Vi har regneregler for hvordan vi stiller opp et regnestykke og hvordan vi regner det ut. Når vi skal vise en utregning må vi sette opp regnestykkene under hverandre og ta hensyn til hvilken plassverdi hvert siffer har.
Overslag
Vi gjør overslag for å regne ut en omtrentlig verdi. Overslag betyr å runde tall opp eller ned for å lette hoderegningen. Det finnes ikke noen eksakt oppskrift på hvordan vi gjør dette, men vi har noen huskeregler.
Vi gjør overslag for å regne ut en omtrentlig verdi. Overslag betyr å runde tall opp eller ned for å lette hoderegningen. Det finnes ikke noen eksakt oppskrift på hvordan vi gjør dette, men vi har noen huskeregler.
|
Addisjon
Vi runder et tall opp og et annet tall ned 27 + 46 --> 30 + 40 |
Subtraksjon
Vi runder et tall opp og et annet tall ned 145 - 74 --> 150 -70 |
Multiplikasjon
Vi runder et tall opp og et annet tall ned 3,8 * 2,4 --> 4 * 2 |
Divisjon
Her runder vi av tallene slik at divisjonen går opp 34: 4--> 32 : 4 |
|
Negative tall
Negative tall er tall lavere enn null, eller sagt på en annen måte; tall med negativ fortegn. Vi skriver ofte negative tall i en parentes. Dette gjør vi for å skille fortegn fra hverandre og og gjøre regningen lettere. Noen eksempler på dette finner du nedenfor. |
|
|
Addisjon og subtraksjon med negative tall
|
Multiplikasjon og divisjon med negative tall
|
Delelighet
Delelighet betyr å finne ut om et tall kan divideres med et annet tall og få et helt tall som kvotient. Nedenfor finner du noen huskeregler som er kjekke å kunne. Tverrsummen av et tall er summen av alle siffer i tallet.
Tallet 483 er delelig på 3 fordi tverrsummen( 4+8+3= 15) er delelig på 3.
Delelighet betyr å finne ut om et tall kan divideres med et annet tall og få et helt tall som kvotient. Nedenfor finner du noen huskeregler som er kjekke å kunne. Tverrsummen av et tall er summen av alle siffer i tallet.
Tallet 483 er delelig på 3 fordi tverrsummen( 4+8+3= 15) er delelig på 3.
|
Delelig med 2
Et tall er delelig med 2 dersom det siste sifferet i tallet er et partall |
Delelig med 3
Et tall er delelig med 3 dersom tverrsummen av tallet er delelig på 3 |
Delelig med 5
Et tall er delelig med 5 dersom det siste sifferet i tallet er 0 eller 5 |
|
Multiplikasjon med tall lavere enn 1
Multiplikasjon med et tall lavere enn 1, gir et produkt som er lavere enn tallet du multipliserte med Multiplikasjon med 0,1 er det samme som å dividere et tall med 10 Multiplikasjon med 0,5 er det samme som å dividere et tall med 2. Multiplikasjon med 0,01 er det samme som å dividere et tall med 100
|
Divisjon med tall lavere enn 1
Divisjon med tall lavere enn 1 gir en kvotient som er høyere enn tallet du diviverte med Divisjon med 0,1 er det samme som å multiplisere et tall med 10 Divisjon med 0,5 er det samme som å multiplisere et tall med 2 Divisjon med 0,01 er det samme som å multiplisere et tall med 100
|
Regnerekkefølge
Regnerekkefølge betyr å ta hensyn til hvilken rekkefølge vi skal gjøre ulike regnearter når vi møter sammensatte oppgaver. Rekkefølgen på regneoperasjonene er som følger:
Regnerekkefølge betyr å ta hensyn til hvilken rekkefølge vi skal gjøre ulike regnearter når vi møter sammensatte oppgaver. Rekkefølgen på regneoperasjonene er som følger:
- Parenteser
- Potenser
- Multiplikasjon og divisjon
- Addisjon og subtraksjon
- 2 + 3*4--> 2 + 12--> 14 ( hadde vi ikke tatt hensyn til denne rekkefølgen og bare regnet fra venstre mot høyre ville vi fått 20)
- 3*2 - 30: 6 + 4 = 6 - 5 +4 = 5 ( hadde vi ikke tatt hensyn ville vi fått 0)
Primtall og primtallfaktorisering
Primtall er tall som kun er delelige på seg selv og 1, og der kvotienten er et helt tall.
De ti første primtallene er 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
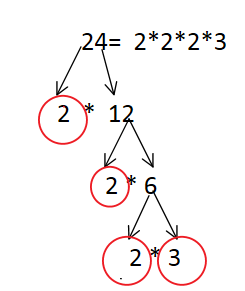
Primtallsfaktorisering går ut på å finne de laveste primtallsfaktorene et tall består av.
Primtall er tall som kun er delelige på seg selv og 1, og der kvotienten er et helt tall.
De ti første primtallene er 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Primtallsfaktorisering går ut på å finne de laveste primtallsfaktorene et tall består av.
|
|
Potenser og tierpotenser
Potenser er en lettere måte å skrive tall på. En potens består av et grunntall og en eksponent. Eksponenten forteller hvor mange ganger et grunntall skal multipliseres med seg selv. En tierpotens er en potens med 10 som grunntall.
Potenser er en lettere måte å skrive tall på. En potens består av et grunntall og en eksponent. Eksponenten forteller hvor mange ganger et grunntall skal multipliseres med seg selv. En tierpotens er en potens med 10 som grunntall.
|
Den første potensen leses som to opphøyd i tre, eller to i tredje. 2 er grunntallet og 3 er eksponenten. Potensen forteller at 2 skal multipliseres med seg selv 3 ganger, altså 2*2*2 = 8
Tallet 8 er potensen skrevet på vanlig måte. Tierpotensen uttales ti i andre, eller ti i tredje. |
|
|
Addisjon og subtraksjon av potenser
Når vi adderer og subtraherer potenser må vi regne ut hver potens for seg og så addere og subtrahere. 
|
Multiplikasjon og divisjon av potenser
Dersom potensene har samme grunntall kan vi addere eller subtrahere eksponentene når vi multipliserer eller dividerer potenser. Dersom grunntallet er ulikt må vi benytte fremgangsmåten med å regne ut hver potens for seg og så addere eller subtrahere. 
|
|
Kvadrattall
Kvadrattall er heltall opphøyd i andre. De ti første kvadrattallene er 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 |
Kubikktall
Kubikktall er et heltall opphøyd i tredje. De ti første kubikktallene er 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000 |
|
|
|
Kvadratrot
Å finne kvadratroten av et tall går ut på å finne hvilket tall som multiplisert med seg selv gir tallet under kvadratrotegnet. 
|
Kubikkrot
Å finne kubikkroten av et tall går ut på å finne hvilket tall som multiplisert med seg selv tre ganger gir tallet under rottegnet. 
|
Desimaltall, brøk og prosent
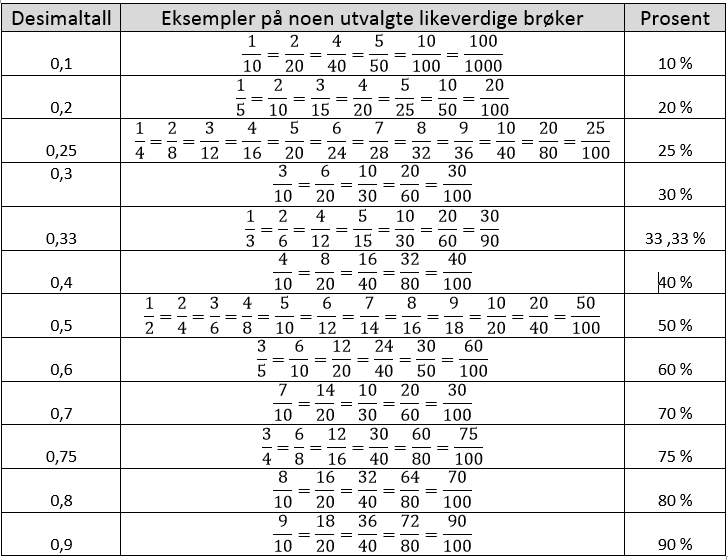
Alle desimaltall kan skrives som brøk og prosent. Alle brøker kan skrives som desimaltall og prosent, og alle prosenttall kan skrives som desimaltall og brøker. Nedenfor følger en liste med desimaltall, brøk og prosent som ofte er i bruk.
Alle desimaltall kan skrives som brøk og prosent. Alle brøker kan skrives som desimaltall og prosent, og alle prosenttall kan skrives som desimaltall og brøker. Nedenfor følger en liste med desimaltall, brøk og prosent som ofte er i bruk.
|
Store tall- Prefikser
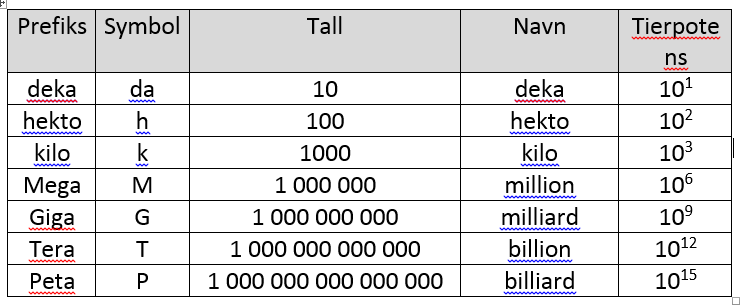
Vi bruker prefikser for å slippe å skrive store tall med alle siffer de inneholder. En prefiks erstatter da deler av tallet slik at det blir enklere å skrive tallet. 
|
Små tall - Prefikser
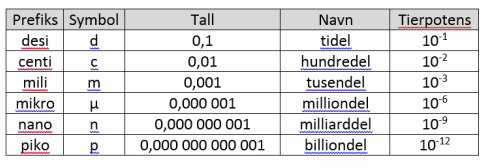
Vi bruker prefikser for å slippe å skrive små talll med alle desimaler de inneholder. En prefiks erstatter da deler av tallet slik at det blir enklere å skrive tallet. 
|
Standardform
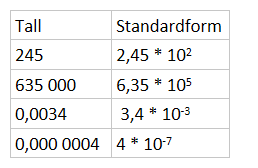
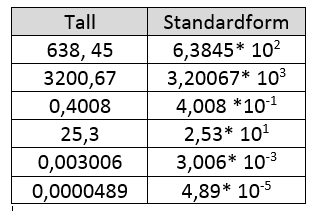
Standardform er en enklere måte og skrive store og små tall på. Standardform består av et tall mellom 1 og 10 multiplisert med en tierpotens. Dersom vi flytter komma mot venstre øker eksponenten og flytter vi komma mot høyre minker eksponenten. Se eksemplene nedenfor.
Standardform er en enklere måte og skrive store og små tall på. Standardform består av et tall mellom 1 og 10 multiplisert med en tierpotens. Dersom vi flytter komma mot venstre øker eksponenten og flytter vi komma mot høyre minker eksponenten. Se eksemplene nedenfor.
|
|
|
Algebra |
|
Uttrykk med og uten variable
Uttrykk uten variable kaller vi talluttrykk. 3 + 10*4 er et eksempel på et talluttrykk.
Uttrykk med variable kalles bokstavuttrykk. 3x + x - 40 er et eksempel på et bokstavuttrykk. De variable er noe som kan variere i verdi.
Uttrykk uten variable kaller vi talluttrykk. 3 + 10*4 er et eksempel på et talluttrykk.
Uttrykk med variable kalles bokstavuttrykk. 3x + x - 40 er et eksempel på et bokstavuttrykk. De variable er noe som kan variere i verdi.
Uttrykk med flere variable
Sette verdier inn i uttrykk med variable
Forenkle uttrykk- Trekke sammen uttrykk
Parentesregning
Faktorisering
Kvadratsetningene
|
Likninger |
|
Flytte- og bytte regelen
|
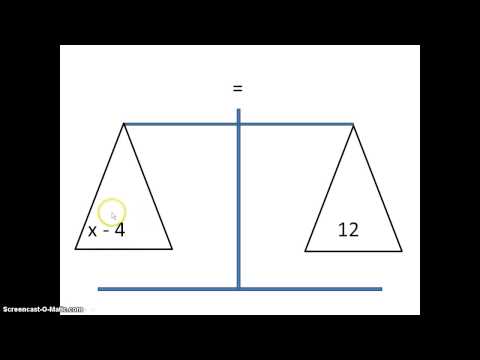
I likningen subtraherer vi venstre side av likningen med 3. Da må vi gjøre dette på høyre side også. Dette prinsippet ligger til grunn for flytte og bytte regelen!
|
Kilder
Sist oppdatert; 21. desember 2015