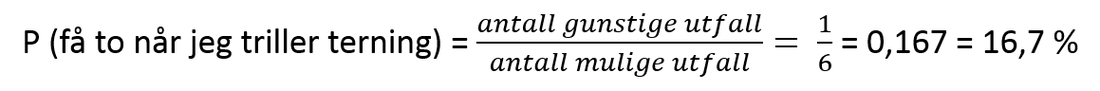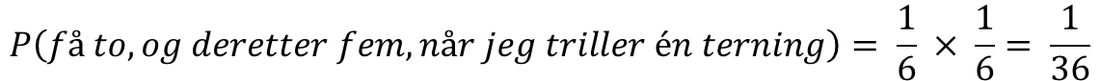SANNSYNLIGHET
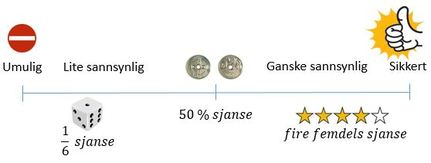
Sannsynlighetsregning går ut på å finne ut hvor sannsynlig det er at noe skal skje (hvor sannsynlig det er at en hendelse inntreffer).

Sannsynlighet beskriver vi ofte med prosent mellom 0 og 100, eller et tall mellom 0 og 1, eller en ekte brøk.
Picture
SANNSYNLIGHETSREGNING MED ÉN TERNING
Et klassisk eksempel er å se på sannsynlighet når vi triller terning. En terning har seks sider, altså seks mulige utfall. Hvis jeg ønsker å regne ut sannsynligheten for å få to når vi triller en terning, er det kun ett gunstig utfall siden det kun er én side på terningen som har to, og dette viser vi slik: 
Vi bruker ofte å skrive P (ønsket hendelse) der P står for probability. Ta deg nå tid til å se på videoen over som forklarer hva sannsynlighet er.
​
Hvis jeg ønsker å regne ut sannsynligheten for å få to eller tre når vi triller en terning, er det to gunstige utfall.
SANNSYNLIGHETSREGNING MED TO TERNINGER
Når vi kaster to terninger, hva er sannsynligheten for at summen av antall øyne ikke blir 10?
Vi finner de 36 mulige utfallene ved å sette opp en tabell. Vi ser at det er enkelt å finne hvor mange utfall som har summen 10; det er tre utfall. Sannsynligheten for at summen blir 10, er 3/36 = 1/12. Siden resten av utfallene gir en annen sum, vil sannsynligheten for summen ikke blir 10, bli 1 - 1/12 = 11/12.
SANNSYNLIGHETSREGNING VED UAVHENGIGE HENDELSER
Vi kaster én terning to ganger. Hva er sannsynligheten for først få en toer, og deretter en femmer?

Når vi skal finne sannsynligheten for to hendelser som er uavhengige av hverandre, multipliserer vi de to sannsynlighetene.
KOMBINATORIKK
Hvor mange muligheter har vi til å lage en en kode på en hengelås med fire valgmuligheter? Vi kan starte med å prøve oss frem. Å jobbe systematisk med tabeller, oppramsing og tegning, for å finne alle løsningene. Når vi har funnet ut hvilket mønster problemet følger, kan vi regne ut antall mulige kombinasjoner, dette er å jobbe med kombinatorikk – vi jobber med å finne ut antall kombinasjoner.
KOMBINASJONSMULIGHETER
Hvor mange muligheter finnes om du skal sette sammen en kø? Eller sette sammen et antrekk med klær du har i klesskapet ditt? Dette kaller vi kombinasjonsmuligheter. Når vi skal stille opp under brannøvelse på fotballbanen, stiller vi oss opp etter klasselista. Hvor mange muligheter har vi egentlig til å stille oss opp i, hvis man kan velge helt selv? Det er mange kombinasjonsmuligheter for oppstilling av en rekke eller kø.
VALGTRE
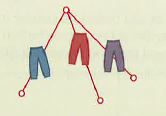
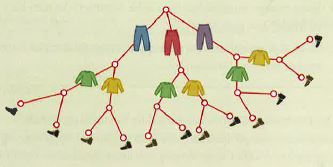
ANTREKKSSITUASJONEN - Hvor mange antrekk kan vi sette sammen?

Tenk deg at du skal på ferie. Du pakker tre bukser, to gensere og to forskjellige par med sko. Hvor mange antrekk kan du da kombinere når du er på ferie?

Da kan vi tegne et valgtre. Først velger vi bukse, vi har da tre muligheter. Valgtreet vårt deler seg da i tre greiner. Vi tegner grenene ut fra et punkt vi kan kalle for «rota».
På hver av disse grenene tegner vi to nye grener, disse nye grenene viser oss hvilke muligheter vi har når vi skal velge genser. Teller vi opp nå, ser vi at vi har seks antrekk å velge mellom, uten å ha tatt med sko.
Vi tegner opp to nye greiner under hver genser, disse skal illustrere hvor mange valg vi kan ta, når vi tar med sko-par.
Hver greinspiss symboliserer et antrekk. Teller vi over, ser vi at ved å ta med oss tre bukser, to gensere og to par med sko, så kan vi sette sammen 12 ulike antrekk.

Multiplikasjonsprinsippet: hvis vi tar 3 bukser, multipliserer med 2 gensere, deretter multipliserer med 2 par sko, så får vi 12 antrekk (3 • 2 ​• 2 = 12).
Bilde
Starten på valgtreet er de tre ulike buksene du kan velge mellom.
Picture
Ferdig tegnet valgtre; tre bukser, to gensere og to forskjellige par med sko.
Her er et eksempel på hvordan vi tegner et valgtre, og kombinerer det med bruk av sannsynlighetsregning.
FAKULTET
3! leses «tre fakultet»
3! står for 3 • 2 • 1 = 6
3! = 6
 
6! står for 6 • 5 • 4 • 3 • 2 • 1 = 720
6! = 720
 
KØSITUASJON
5 venner drar på kino, hvor mange forskjellige seteplasseringer kan de ha?
Når vi skal ordne en kø, med 5 mennesker, har vi 5! muligheter.
Når 1 person av totalt 5 personer er plassert, har du 4 igjen å plassere, og fire seter igjen å velge mellom.
Når 2 personer av totalt 5 personer er plassert, har du 3 igjen å plassere, tre og seter igjen å velge mellom.
Når 3 personer av totalt 5 personer er plassert, har du 2 igjen å plassere og to valgmuligheter.
Når 4 personer av totalt 5 personer er plassert, har du 1 person igjen å plassere, og kun ett valg.
 
Dette kan vi regne ut på følgende måte: 5!
5! = 5 • 4 • 3 • 2 • 1 = 120
For å plassere 5 mennesker etter hverandre, har vi 5! valg, altså 120 mulige kombinasjoner.
MEDALJESITUASJONEN
I eksempelet over, der alle vennene skulle på kino og få en plass i kinosalen, skulle ALLE med.
Dette er ikke tilfelle om det kun er noen tilfeldig valgte som får plasser i kinoen.
Tenk deg en konkurranse i lengdehopp, der det var 6 deltagere, men det er kun tre av dem som får «pallplassering», altså medaljer i konkurransen.
Her er det ganske lik tankegang som da vi delte ut kinobilletter til alle vennene.
Tenk først, at du velger ut gullvinneren, da har vi 6 mulige vinnere, siden det er 6 deltakere i konkurransen. Deretter velger vi ut sølvvinneren, da har vi 5 mulige personer som kan få sølvmedalje. Til bronsjemedaljen er det kun fire valgmuligheter. Totalt antall kombinasjoner da, er 6 • 5 • 4 = 120 mulige kombinasjoner.
I «medaljesituasjonen» har vi færre å velge mellom enn i køsituasjonen. Når vi har valgt den første, har vi én mindre ved neste valg.
Kildehenvisninger
http://design.tutsplus.com/tutorials/how-to-create-shiny-vector-dice-in-illustrator--vector-2354
https://weekly.blog.gustavus.edu/2013/03/22/lincoln-gets-high-marks-with-broad-audience/
http://www.norges-bank.no/Sedler-og-mynter/Mynter/1-kronemynten/
http://www.trafikkskilt.no/images/forbudsskilt/innkjoring_forbudt.jpg
http://thevoiceofone.org/2015/02/04/thumbs-up/
Lektor DTs mattevideoer
Kenneth Nygaard (youtube)
Sofie Aarnes (youtube)
campus.inkrement.no
NUMMER 9 - Aschehoug

Oppdatert
7. mars 2016